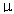 e desvio
padrão
e desvio
padrão 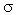 ,
fazem-se várias amostras do mesmo tamanho N (figura
1) Para cada uma
dessas amostras é possível calcular a respectiva média
(
,
fazem-se várias amostras do mesmo tamanho N (figura
1) Para cada uma
dessas amostras é possível calcular a respectiva média
(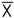 ) (Quadro
1).
) (Quadro
1). A importância que a distribuição Normal tem na estatística deve-se em parte ao resultado que em seguida vai ser explicado.
Suponhamos que de uma população
com média 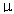 e desvio
padrão
e desvio
padrão 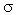 ,
fazem-se várias amostras do mesmo tamanho N (figura
1) Para cada uma
dessas amostras é possível calcular a respectiva média
(
,
fazem-se várias amostras do mesmo tamanho N (figura
1) Para cada uma
dessas amostras é possível calcular a respectiva média
(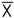 ) (Quadro
1).
) (Quadro
1).
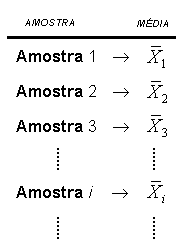 Quadro 1 |
Pelo Teorema
do Limite Central, a distribuição das médias destas amostras
tende para uma distribuição normal com média 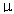 (igual á média da população) e com desvio padrão
(igual á média da população) e com desvio padrão
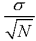 (desvio
padrão da população a dividir pela raiz quadrada do tamanho
das amostras).
(desvio
padrão da população a dividir pela raiz quadrada do tamanho
das amostras).
Observemos o seguinte exemplo: vamos considerar como população de 1375 os índividuos internados num hospital por apendicite. A distribuição do tempo desse internamento da população está representada pelo histograma na figura 2 . Pode-se observar que a média e o desvio padrão do tempo de internamento nesta população são respectivamente 6 e 5,46.
Suponhamos
então que se fazem 200 amostras de tamanho N=100 e para cada uma
dessas amostras a média é calculada. A figura
3 mostra a distribuição das 200 médias. Note-se que
o histograma começa a aproximar-se de uma distribuição
normal, bem como a média (6,4) é já bastante semelhante
à média da população (6). Também o desvio
padrão da distribuição das médias (0,56) já
se aproxima muito do valor previsto pelo teorema do limite central (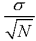 =
5,46/10 = 0,55). Se o número de amostras feitas fosse maior todas estes
valores tornariam-se mais precisos.
=
5,46/10 = 0,55). Se o número de amostras feitas fosse maior todas estes
valores tornariam-se mais precisos.
Ao desvio padrão
da distribuição das médias amostrais (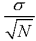 )
dá-se o nome de erro padrão da média.
)
dá-se o nome de erro padrão da média.
Toda a descrição anterior é apenas teórica e o que num estudo se tem é apenas uma amostra de uma população. A importância do resultado é sabermos calcular qual a variabilidade das amostras dessa população - o erro padrão. Se o erro padrão for pequeno as amostras com médias semelhantes à média da população são mais frequentes e assim é mais provável que a amostra que obtivemos seja uma dessas amostras.
O erro padrão pode ser controlado com o tamanho da amostra. Quanto maior for o tamanho da amostra menor será o erro padrão.