Estatística Descritiva

Variáveis quantitativas

Os dados apresentados nos exemplos deste capítulo constam da base de dados alchool.sav.

Figura 1 - Histograma representando a distribuição da variável "peso à nascença"

Os métodos para sumariar variáveis contínuas e discretas são os mesmos. No entanto, poderá haver situações nas quais poderá ser mais informativo usar tabelas de frequências ou gráficos de barras para variáveis discretas, nomeadamente quando existem, na prática, poucos valores que a variável discreta pode assumir (por exemplo, número de filhos).

De uma geral, a tabela de frequências não é, muito útil para descrever ou sumariar variáveis quantitativa pois grande parte dos valores terão frequência 1. Assim, a tabela de frequências seria uma grande lista de valores pouco menos complexa que a totalidade dos dados da variável. Da mesma forma, um gráfico de barras para dados quantitativos seria composto por uma séria de pequenas barras. Uma melhor opção a este gráfico é o histograma. O histograma é semelhante ao gráfico de barras com a diferença que cada barra representa a frequência de um intervalo de valores. Cada intervalo de valores tem a continuação no intervalo da barra seguinte. Por isso as barras são representadas todas juntas.

(como obter o histograma no SPSS?)

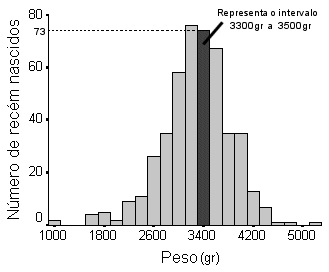
Na figura 1, o histograma refere-se ao peso à nascença de 462 recém nascidos. A barra mais escura representa o número de recém nascidos (setenta e três) com peso entre os 3300gr e 3500gr.

Figura 2 - Histograma com a indicação da mediana relativa à variável "peso à nascença"

As variáveis quantitativas podem também ser sumariadas usando medidas de sumário. A média é um exemplo bem conhecido destas medidas (a média é em particular uma medida de posição e, dentro destas, uma medida de tendência central). Uma forma de sumariar os peso dos 462 recém nascidos é apresentar o peso médio, 3263gr. Este valor é calculado somando os 462 pesos e dividindo por 462.

Outra medida de tendência central é a mediana. A mediana indica o centro da distribuição da variável, ou seja, é o valor acima do qual estão 50% dos valores da variável e abaixo os restantes 50%.

Uma forma simples de calcular a mediana é ordenando todos os valores sendo a mediana o valor central. Por exemplo, para calcular oa mediana do conjunto 4, 2, 3, 2, 7 vamos primeiro ordená-lo: 2, 2, 3, 4, 7. O valor do meio é o 3, então 3 é a mediana do conjunto.

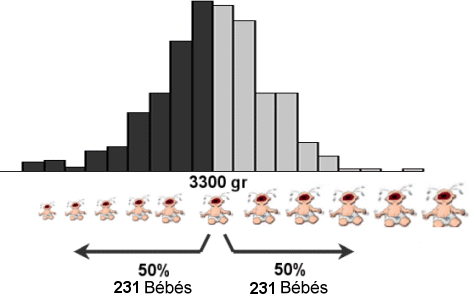
Na figura 2 está representada a distribuição do peso de 462 recém nascidos. A mediana neste caso é 3300gr, o que quer dizer que 50% dos recém nascidos (231 recém nascidos) têm um peso inferior a 3300gr e os restantes 50% têm um peso superior a 3300gr.

O conceito da mediana pode ser generalizado para outras percentagens além dos 50%. Por exemplo, podemos querer saber qual é o valor abaixo do qual estão 10% dos indivíudos. A esta medida de posição dá-se o nome de percentil 10. A mediana é portanto, o percentil 50. Alguns percentis têm uma designação especial. Por exemplo o percentil 25 e o percentil 75 são referidos como o 1º quartil e o 3º quartil, respectivamente.

Figura 3 - Histograma com a indicação dos percentis 5 e 95 relativos à variável "peso à nascença"

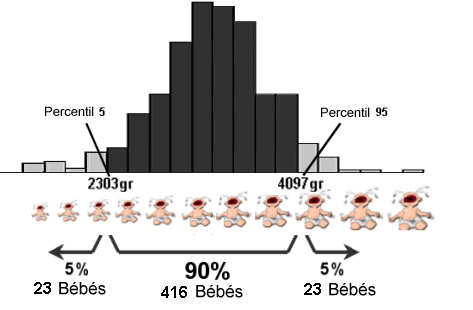
No exemplo dos 462 recém nascidos os percentis 5 e 95 são respectivamente 2303gr e 4097gr. Isto quer dizer que 90% dos recém nascidos têm o peso compreendido entre as 2303gr e 4097gr como está indicado na figura 3.

 Outro tipo de medidas de sumário são usadas para indicar o grau de dispersão dos dados; estas medidas designam-se por medidas de dispersão. O desvio padrão é um exemplo destas medidas e indica a variação dos dados à volta da média.

A tabela 1 apresenta alguns exemplos dos desvio à média dos pesos à nascença dos 462 recém nascidos. O desvio padrão é uma medida que resume todos estes desvios a um único valor, neste caso 553.5gr. 

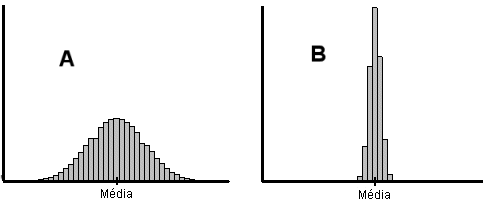
Os dois histogramas da figura 4 referem-se a dados com a mesma média mas com diferentes dispersões à volta dos mesmos. Os dados referentes ao histograma A têm uma maior dispersão do que os do histograma B, assim o desvio padrão do A é maior do que o B.

A diferença entre dois percentis pode também ser usada para descrever a variação dos dados. A esta medida dá-se o nome de âmbito (range). Por exemplo o âmbito dos percentis 5 e 95 do peso dos 463 recém nascidos 1794 gr. (4097gr - 2303gr). Um dos âmbitos mais usados é o âmbito interquartil, ou seja, a diferença entre o percentil 75 e 25.

Figura 4 - Distribuição de duas variáveis com a mesma média mas com desvios padrões diferentes.  A variável A tem maior dispersão do que a B

(como obter medidas de sumário no SPSS?)

A escolha das medidas de posição e dispersão apropriadas

Um dos factores que se deve ter em conta na escolha das medidas a usar é o tipo de distribuição da variável.

A média é mais informativa do que a mediana pois no seu cálculo são utilizados os valores da variável, enquanto no cálculo da mediana apenas se usa a posição relativa de cada valor. Consideremos o seguinte conjunto de valores como exemplo,

2, 4, 5, 6, 8

A média é (2+4+5+6+8)/5 = 5 e a mediana também é 5. Mas se alterarmos o último valor para 23, isto é

2, 4, 5, 6, 23

a mediana continua a ser 5 mas a média foi alterada para 8.

Neste exemplo pode-se observar que a média é mais afectada por valores extremos do que a mediana. Em situações em que a variável apresenta valores muito extremos, deve-se optar pela mediana dando assim uma idicação mais correcta da zona central da distribuição. Uma regra geral muitas vezes utilizada é apresentar a média em distribuições simétricas e a mediana em distribuições assimétricas.

Relativamente às medidas de dispersão, estas dever ser escolhidas em função da medida de tendência central. O desvio padrão só deverá ser apresentado se estiver associado à média, uma vez que esta medida se refere aos desvios à média. No caso de se apresentar a mediana poder-se-á optar por indicar o âmbito, por exemplo interquartil, ou apresentar dois pecentis. Os pares de percentis mais frequentemente usados são o (percentil 5, percentil 95) e o (percentil 25, percentil 75).